สวัสดีน้องๆ ชาว #dek62 อ่านฟิสิกส์เป็นไงบ้างคะคำนวณปวดหัวไหม วันนี้พี่บิวจะพาน้องๆ ทำโจทย์ฟิสิกส์ที่ไม่มีตัวเลขเรื่องของไหล ในข้อสอบ PAT2 มีโจทย์ลักษณะนี้หลายข้อและไม่ยาก แต่น้องๆ ต้องแม่นสูตรนิดนึง ทำโจทย์ที่ไม่มีตัวเลขง่ายกว่ายังไงมาดูกันค่ะ
ทบทวนสูตรของไหล

โดยที่ \(\rho\) คือ ความหนาแน่น (\(kg\)/\(m^3\))
\(m\) คือ มวล (\(kg\))
\(P\) คือ ความดัน (\(Pa\) ,\(N\)/\(m^2\))
\(F\) คือ แรงที่ของเหลวกระทำต่อวัตถุ (\(N\))
\(A\) คือ พื้นที่ (\(m^2\))
\(\gamma\) คือ ความตึงผิว (\(N/m\))
\(l\) คือ ความยาวของวัตถุที่สัมผัสกับของเหลว
\(\eta\) คือ สัมประสิทธิ์ความหนืด
ตัวอย่างโจทย์ PAT2 มี.ค.60
หลอดไพทอทที่ติดอยู่บนลำตัวเครื่องบินมีลักษณะเป็นท่อปลายแหลม ใช้วัดอัตราเร็วของอากาศเทียบกับเครื่องบิน หลอดดังกล่าวประกอบด้วยท่อทรงกระบอกสองอันซ้อนกัน โดยปลายด้านหน้าเชื่อมติดกันเป็นปลายแหลมและเจาะรูที่ทรงกระบอกนอกดังรูป เมื่อเครื่องบินเคลื่อนที่ อากาศจะไหลเข้าปะทะปลายท่อและเบนออกไปด้านข้างผ่านรูที่เจาะไว้(แต่ไม่ได้เข้าไปในรู) ดังนั้นอากาศที่บริเวณ \(P_1\) และ \(P_2\) จึงเป็นอากาศที่นิ่งแต่มีค่าแตกต่างกัน ที่ปลายทรงกระบอกตัวในติดตั้งตัววัดผลต่างความดันไว้ซึ่งใช้คำนวณหาอัตราเร็วของอากาศ
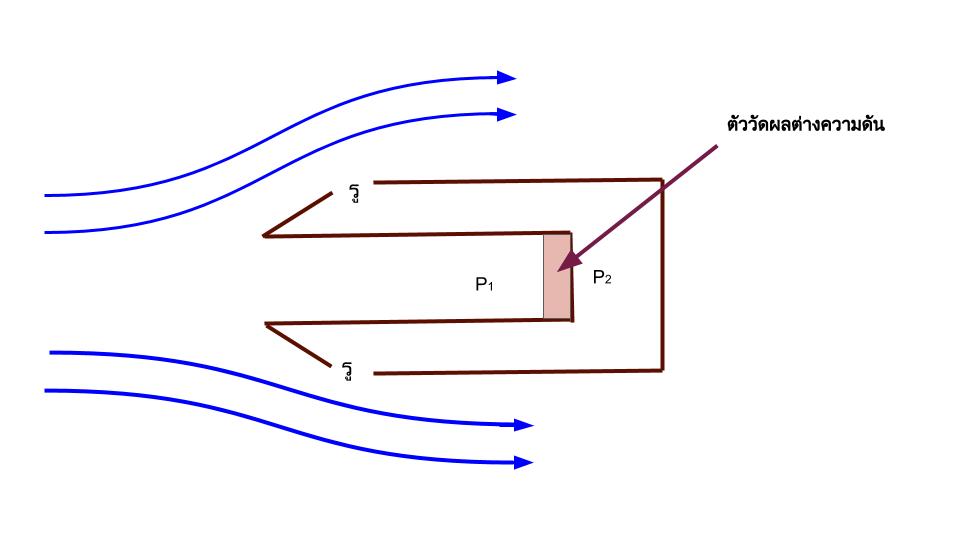
สมการข้อใดเขียนถูกต้อง กำหนดให้ \(P_1\) และ \(P_2\) เป็นความดันของทั้งสองบริเวณ , \(\rho\) เป็นความหนาแน่นอากาศ ,\(v\) เป็นอัตราเร็วของอากาศเทียบกับท่อไพทอท และ \(h\) เป็นระดับความสูงเครื่องบินเทียบกับระดับน้ำทะเล
1. \(P_1-P_2\) \(={\frac{1}{2}}\rho{v^2}\)
2. \(P_2-P_1\) \(={\frac{1}{2}}\rho{v^2}\)
3. \(P_1-P_2\) \(={\frac{1}{2}}\rho{v^2}\) \(+{\rho}gh\)
4. \(P_-P_1\) \(={\frac{1}{2}}\rho{v^2}\) \(+{\rho}gh\)
5. ไม่มีข้อมูลใดถูกต้อง
โจทย์กำหนด \(P_1\) ,\(P_2\) ,\(\rho\) ,\(v\) ,\(h\) โจทย์ถามว่าสมการในข้อใดอธิบายสิ่งที่เกิดขึ้นนี้
ถ้าน้องๆ อ่านโจทย์แล้วไม่รู้ว่าควรใช้สูตรไหน พี่บิวแนะนำว่าให้น้องดูตัวแปรว่ามีในสูตรใดบ้าง อย่างโจทย์ข้อนี้จะมีในสมการแบร์นูลลีทุกตัวเลย ดังนั้น พี่บิวจะแทนตัวแปรลงไปในสมการแบร์นูลลีเลย
จากสมการแบร์นูลลี \(P_1\) \(+{\frac{1}{2}}\rho{v_1}^2\) \(\rho{g}h_1\)\(={P_2}\) \(+{\frac{1}{2}}\rho{v_2}^2\) \(+{\rho}g{h_2}\)
วิเคราะห์ตัวแปร \(P_1\) และ \(P_2\) โจทย์กำหนดให้ มีความดันทั้งสองที่ และไม่เท่ากัน
\(v_1\) เป็นความเร็วภายนอกท่อ แสดงว่ามีการเคลื่อนที่ของอากาศ
\(v_2\) คืออากาศภายในท่อ แสดงว่าไม่มีการเคลื่อนที่ของอากาศ ดังนั้น \(v_2\) เป็น 0
\(h_1 \) และ \(h_2 \) คือความสูง และความสูงของทั้ง 2 บริเวณเท่ากัน ดังนั้น \(h_1 \) =\(h_2 \) พี่บิวจะแทนลงไปในสูตรเป็น \(h\) เลยนะคะ
แทนค่าสูตรและแก้สมการได้เลย
\(P_1\) \(+{\frac{1}{2}}\rho{v_1}^2\) \(\rho{g}h\) \(={P_2}\) \(+{\frac{1}{2}}\rho{(0)}^2\) \(+{\rho}g{h}\)
\(P_1\) \(+{\frac{1}{2}}\rho{v_1}^2\) \(+{\rho}g{h}\) \(={P_2}\) \(+{\rho}g{h}\)
\({\frac{1}{2}}\rho{v_1}^2\)\(+{\rho}g{h}\)\(-{\rho}g{h}\) \(={P_1-P_2}\)
\({P_1-P_2}\)\(={\frac{1}{2}}\rho{v_1}^2\)
จะได้คำตอบเป็นตัวเลือกที่ 2 ไปค่ะ
แค่รู้สูตรก็แทนค่าแก้สมการได้แล้ว โจทย์อาจจะยาวมากไปหน่อยแต่ถ้าน้องๆ สแกนหาตัวแปรและแทนค่าสูตรได้ ก็ได้คำตอบแล้วค่ะ หากน้องๆมีข้อสงสัยหรือมีข้อเสนอแนะใดๆ สามารถเข้ามาพูดคุยกันได้ที่ line @schooldekd หรือ facebook : schooldekd
และถ้าน้องๆอยากจะแม่นเรื่องของไหลขึ้นอีกสามารถสมัครเรียนได้ที่ พิชิต TCAS – ของไหล ความร้อน อะตอมนิวเคลียร์ สอนโดย สอนโดย อ.หลิน อาจารย์ประจำภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย ที่จะสอนพร้อมสอดแทรกเทคนิคการทำโจทย์ และชี้จุดควรระวังในการทำข้อสอบให้กับน้องๆ ด้วย ได้เรียนกับตัวจริงด้านฟิสิกส์แบบนี้ พลาดไม่ได้เลยนะคะ



