อีกเดือนนิดๆ น้องๆ ม.ุ6 ก็จะต้องสอบ PAT1 กันแล้ว วันนี้พี่บิวมีเทคนิคลับๆ ที่โรงเรียนไม่ได้สอนน้องๆ มาให้ทุกคนเหมือนเดิม บอกเลยว่าเทคนิคนี้จะช่วยให้น้องๆ ทำข้อสอบเรื่องลิมิตที่ออกสอบทุกปีได้แบบสบายๆ เทคนิคที่พี่บิวจะสอนในวันนี้ก็คือ กฏโลปิตาล (L’Hospital’s Rule)
กฏโลปิตาล คืออะไร ?
ในการแก้โจทย์ลิมิตตามปกติแล้ว เราจะต้องจัดรูปพหุนาม แยกตัวประกอบ และการคอนจูเกต ซึ่งจะใช้เวลาเยอะ และถ้าน้องๆ จัดรูปสมการไม่คล่อง โจทย์ลิมิตก็จะเป็นเรื่องยากไปเลย กฏโลปิตาลที่พี่บิวจะแนะนำวันนี้จะช่วยให้น้องๆ ทำโจทย์ลิมิตได้ง่ายขึ้น เพราะโลปิตาลจะให้เราดิฟโจทย์ตรงๆ ไปได้เลย และสูตรดิฟก็ไม่ยากมากด้วย
ทบทวนสูตรอนุพันธ์ (Differentiation) กันก่อน
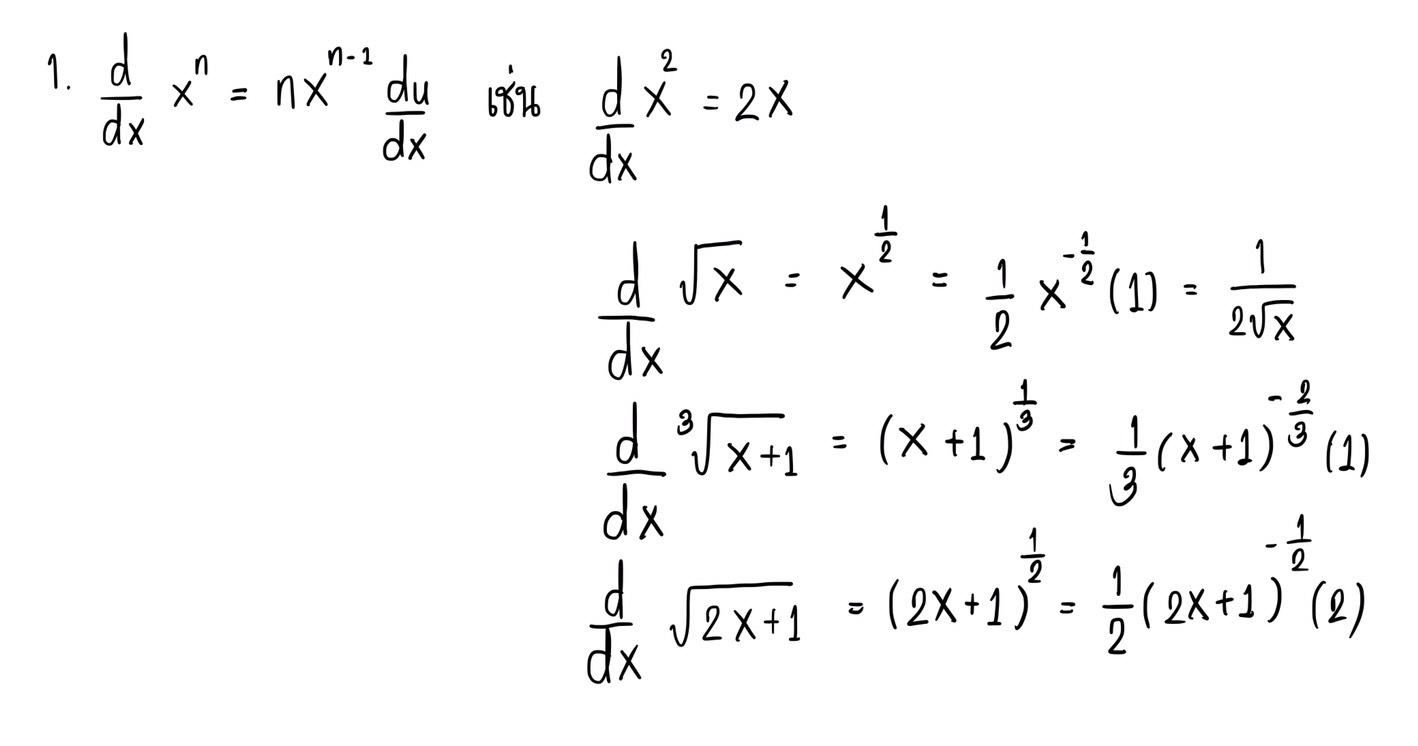
สูตรดิฟหลักๆ ที่เจอในข้อสอบ PAT1 จะใช้อยู่สูตรเดียว ถ้าน้องๆ เจอสมการพหุนามที่ติดรูท เราสามารถเปลี่ยนให้เป็นกำลัง \( \frac{1}{2}\) แล้วดิฟแบบปกติได้เลย
ใช้กฏโลปิตาลแก้โจทย์ยังไง
ถ้าเราแทนค่าลิมิตแล้ว ลิมิตอยู่ในรูป \( \frac{0}{0}\), \( \frac{∞}{∞}\), \(∞-∞\), \(0.∞\), \(0.∞\), \(0.0\), \(1.∞\), \(0^∞\) เราจะใช้กฏโลปิตาลช่วยในการแก้โจทย์ แต่ในข้อสอบ PAT 1 มักจะออกกรณี \( \frac{0}{0}\) หรือ \( \frac{∞}{∞}\) ตลอด ดังนั้นพี่บิวขอพูดถึงวิธีทำโจทย์ที่เข้าเงื่อนไขนี้เท่านั้นนะคะ
กรณีที่ลองแทนค่าหาลิมิตในสมการพหุนามแล้วได้ \( \frac{0}{0}\) หรือ \( \frac{∞}{∞}\) เราสามารถดิฟโจทย์ของตัวเศษและตัวส่วนได้เลย
ตัวอย่างโจทย์
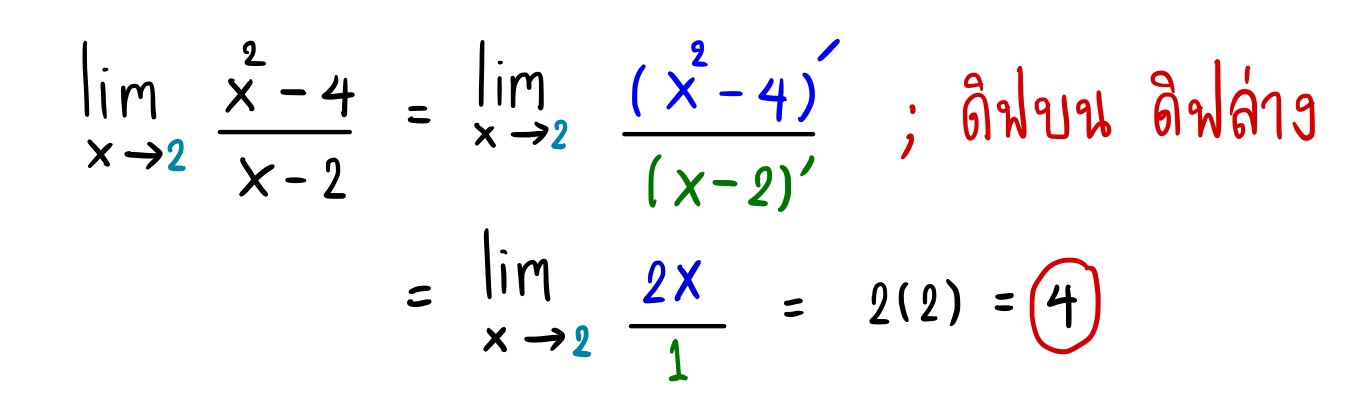
จากโจทย์เราสามารถดิฟตัวเศษ \(x^2-4\) กับดิฟตัวส่วน \(x-2\) ได้เลย แล้วจึงแทนค่าลิมิตลงไป ก็จะได้คำตอบออกมาค่ะ
โลปิตาลในข้อสอบ PAT1
ข้อสอบ PAT1 มักจะดักทางเราด้วยการตั้งโจทย์ที่มี ฟังก์ชันเอกซ์โพเนนเชียล(Exponential Function) เช่น \(2^x\) หรือ \(2^{\sqrt {x}}\) ซึ่งการดิฟฟังก์ชันเอกซ์โพเนนเซียลนั้นทำได้ยาก พี่บิวแนะนำให้น้องๆ ดึงตัวร่วมส่วนที่เป็นเอกซ์โพเนนเซียลออกมาก่อน แล้วถึงทำการโลปิตาล มาลองทำโจทย์ไปพร้อมๆ กันนะข้อสอบจริง PAT1 มีนาคม 2560
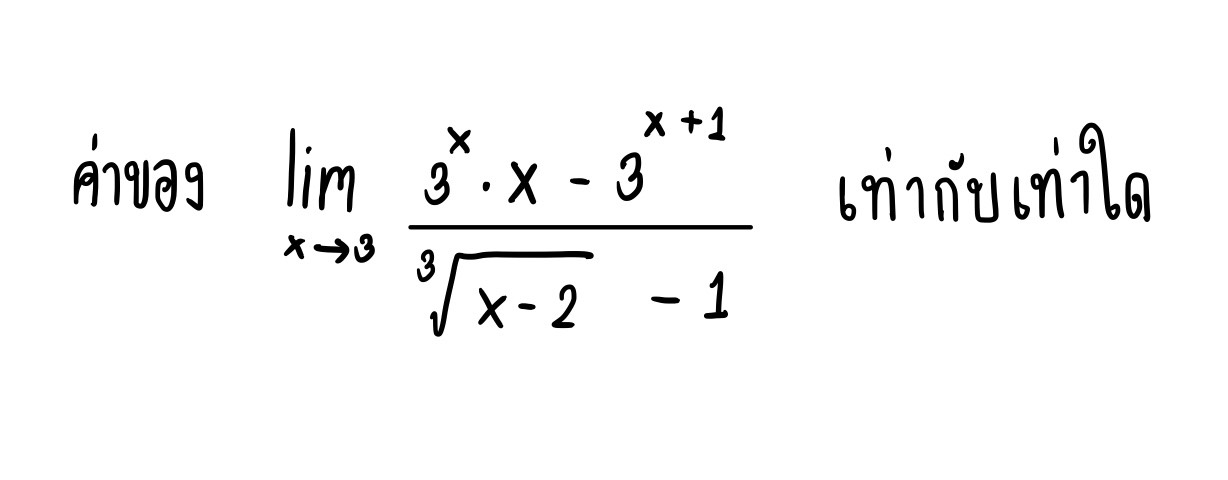
อันดับแรกเราลองแทนค่าลิมิตลงไปในโจทย์ก่อนเพื่อเช็คว่าค่าลิมิตมีค่าเป็น \( \frac{0}{0}\) ตามเงื่อนไขของเทคนิคโลปิตาลมั้ย
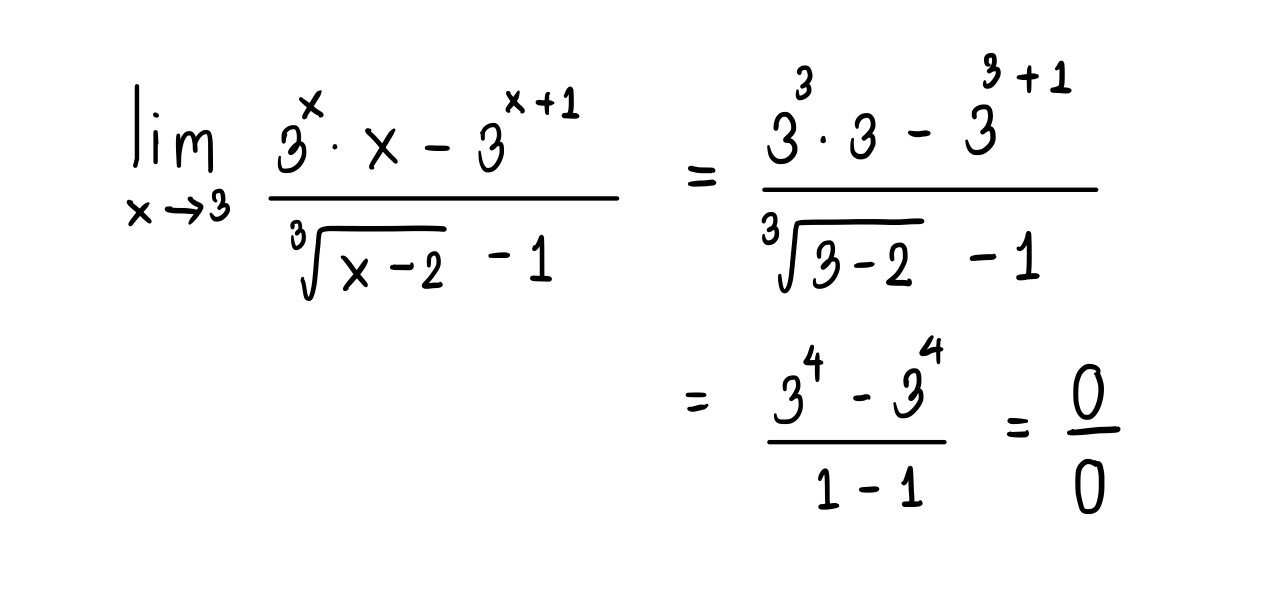
เมื่อเช็คว่าสมการเข้าเงื่อนไขแล้ว คราวนี้เรามาลองใช้กฏโลปิตาลแก้โจทย์กัน

จากตัวอย่างพี่จะดึง \(3^x\) ซึ่งเป็นเอกซ์โพเนนเซียลออกมาก่อน แล้วก็ทำการดิฟส่วนที่เหลือ นั่นคือ ตัวเศษเหลือ \(x-3\) กับตัวส่วนเหลือ \(\sqrt [3]{x-2}\) เมื่อทำการดิฟแล้วแทนค่าลิมิตเท่ากับ 3 ดังนั้นคำตอบข้อนี้เป็น 81
ทำโจทย์โดยใช้เทคนิคไปแล้ว คราวนี้พี่บิวจะลองแก้โจทย์ข้อนี้แบบวิธีตรงไปตรงมาดู มาดูกันว่าคำตอบจะเท่ากันไหม?

จะเห็นว่าได้คำตอบเท่ากันทั้ง 2 วิธี แต่โลปิตาลจะง่ายและใช้เวลาน้อยกว่า น้องๆ จะได้มีเวลาเหลือเพื่อไปทำข้อสอบข้ออื่นได้อีกค่ะ
น้องๆ น่าจะเข้าใจเทคนิคนี้กันแล้วเนอะ งั้นมาลองทำข้อสอบ PAT1 ข้ออื่นเรื่องลิมิตด้วยเทคนิคโลปิตาลกันดู ได้คำตอบเท่ากันหรือไม่อย่างไร สามารถแสดงความคิดเห็นมาได้เลยค่ะ
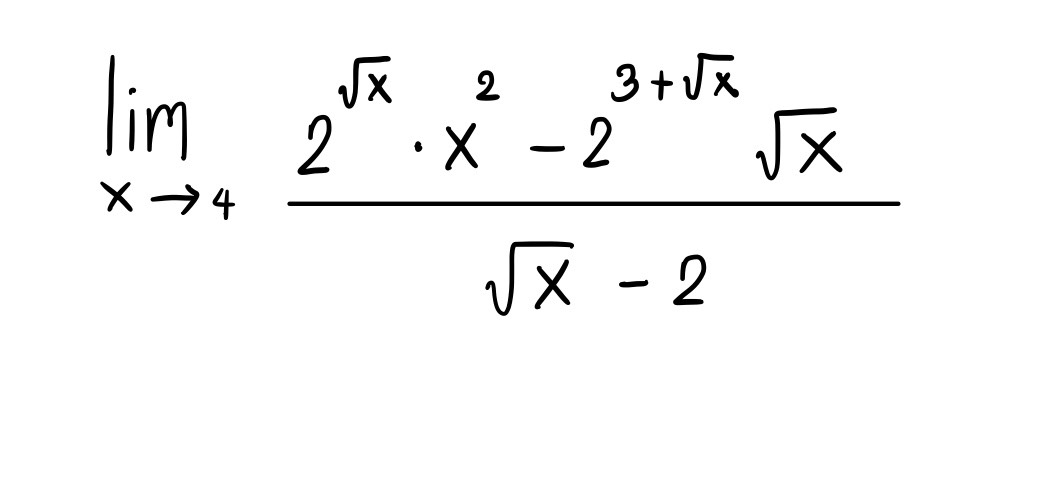
(เฉลยคำตอบข้อนี้คือ 96)
ถ้าน้องๆมีข้อเสนอแนะ หรือวิธีการแก้โจทย์ที่เจ๋งกว่านี้ สามารถมาแสดงความคิดเห็นด้านล่างได้เลยค่ะ หรือ inbox สอบถามมาที่ facebook : schooldekd หรือ Line @schooldekd ได้เลยค่ะ
และถ้าน้องๆคนไหนที่ต้องการเตรียมตัวให้พร้อมสำหรับการสอบ TCAS ในเรื่อง อนุกรม แคลคูลัส และ กำหนดการเชิงเส้น กับอาจารย์กิ๊ฟ ผศ.ดร.วิทวัชร์ โฆษิตวัฒนฤกษ์ อาจารย์ประจำภาควิชาคณิตศาสตร์ ม.มหิดล ที่มีประสบการณ์การสอนคณิตศาสตร์ในระดับมัธยมศึกษาจนถึงปริญญาเอกทั้งในและต่างประเทศมากกว่า10 ปี ทั้งยังเป็นตัวแทนประเทศไทยแข่งคณิตศาสตร์โอลิมปิก 3 สมัย สามารถดูรายละเอียดเพิ่มเติมและสมัครเรียนได้ที่ พิชิต TCAS – แคลคูลัส (ลำดับและอนุกรม แคลคูลัส) โอกาสที่จะได้เรียนกับตัวจริงด้านคณิตศาสตร์แบบนี้มีไม่บ่อย ห้ามพลาดนะคะ




