ทวงคืนคะแนน PAT1 เรขาคณิตวิเคราะห์

ใกล้เข้ามาเรื่อยๆ แล้วกับการสอบ PAT1 พร้อมกันหรือยังคะ ถ้ายังไม่พร้อมไม่เป็นไร วันนี้พี่บิวจะพาน้องๆ ไปทวงคะแนน PAT1 เรื่องเรขาคณิตวิเคราะห์ ออกสอบ PAT1 ปีละประมาณ 3-5 ข้อ เรื่องนี้เนื้อหาอาจจะดูเยอะ แต่ก็มีข้อที่สามารถเก็บคะแนนได้ง่ายเหมือนกัน ง่ายยังไงมาดูกันเลยค่ะ

ทบทวนสูตรเรขาคณิตวิเคราะห์

เส้นตรง $y=mx+c$
-ความชัน
-ตัดแกน  $y$ ที่ $c$

เส้นตรง $Ax+By+C = 0$
-ความชัน $\frac{-A}{B}$

เส้นตรงที่ผ่าน ($x_1$ , $y_1$) และ ($x_2$ , $y_2$)
-ความชัน $\frac{y_1-y_2}{x_1-x_2}$
-สมการ $\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}$  คือ ความชัน

ตัวอย่างโจทย์ PAT1 ต.ค.59

กำหนดเส้นตรง $3x-4y-6=0$ ตั้งฉากกับเส้นตรง $x+ay+3=0$ เมื่อ $a$ เป็นจำนวนจริง ถ้าเส้นตรงทั้งสองตัดกันที่จุด $A$ และตัดแกน $x$ ที่จุด $B$ และจุด $C$ ตามลำดับ แล้วพื้นที่รูปสามเหลี่ยม $ABC$ ตรงกับข้อใด

1. 6 ตารางหน่วย
2. 8 ตารางหน่วย
3. 10 ตารางหน่วย
4. 12 ตารางหน่วย
5. 14 ตารางหน่วย

โจทย์ต้องการพื้นที่รูปสามเหลี่ยม จากสูตรพื้นที่สามเหลี่ยม คือ $\frac{1}{2}$ (ฐาน)(สูง) แต่เรายังไม่สามารถแทนค่าสูตรลงไปได้เลย เพราะเรายังไม่รู้ค่าของฐานและความสูง เราจะหาฐานและความสูงจาก เส้นตรง 2 เส้นที่โจทย์กำหนดให้

จากเส้นตรง 2 เส้น $3x-4y-6=0$ กับ $x+ay+3=0$ ที่ตั้งฉากกัน หมายความว่าความชันของทั้งสองสมการคูณกันได้ -1

จากเส้นตรง $3x-4y-6=0$ และจากสูตร ความชัน  $={\frac{-A}{B}}$ จะได้ความชันคือ $={\frac{-3}{-4}}={\frac{3}{4}}$และจากเส้นตรง  $x+ay+3=0$ และความชันของทั้งสองสมการคูณกันได้ -1

ดังนั้น ความชันของ $x+ay+3=0$ คือ ${(\frac{3}{4})(\frac{-1}{a})}= -1$

                                                       ${\frac{-3}{4}}a=-1$

         $-3=-4a$

         $a={\frac{3}{4}}$

จะได้สมการนี้คือ $x+{\frac{3}{4}}y+3=0$ หรือ คูณ 4 ทั้งสมการเป็น $4x+3y+12=0$

หาจุด B โจทย์บอกว่า เส้นตรง $3x-4y-6=0$ ตัดแกน $x$ ที่จุด $B$ นั่นคือ $y=0$

$3x-4(0)-6=0$
$3x-6=0$
$x=2$

ดังนั้น จุด B คือ (2,0)

หาจุด C โจทย์บอกว่า เส้นตรง  $x+{\frac{3}{4}}y+3=0$ ตัดแกน $x$ ที่จุด $C$ นั่นคือ $y=0$

$x+a(0)+3=0$
$x+3=0$
$x=-3$

ดังนั้น จุด C คือ (-3,0)

หาจุด A  หาได้จากการแก้สมการเส้นตรงทั้งสองเส้น

จากสมการเส้นตรงทั้งสอง $3x-4y-6 = 0 ………..(1)$
$4x+3y+12 =0……….(2)$

การแก้สมการ 2 ตัวแปร เราต้องกำจัดตัวแปรใดตัวแปรนึงหายไปก่อน ในข้อนี้พี่จะกำจัดตัวแปร $x$ นะคะ
ก่อนอื่นก็ทำสัมประสิทธิ์หน้า $x$ ให้เท่ากัน

จาก (1) คูณกับ 4 จะได้ $12x-16y-24 = 0……….(3)$
จาก (2) คูณกับ 3 จะได้ $12x-9y+36 = 0………..(4)$

นำ (4)-(3) จะได้ $25y+60 = 0$
$25y = -60$
$y= {\frac{-12}{5}} = -2.4$
จะได้ ค่า $y$ ของจุด $A$ คือ ${\frac{-12}{5}}$ หรือ $-2.4$

นำจุดทั้งหมดของ $A$ $B$ $C$ มาวาดกราฟ จะได้ดังรูป

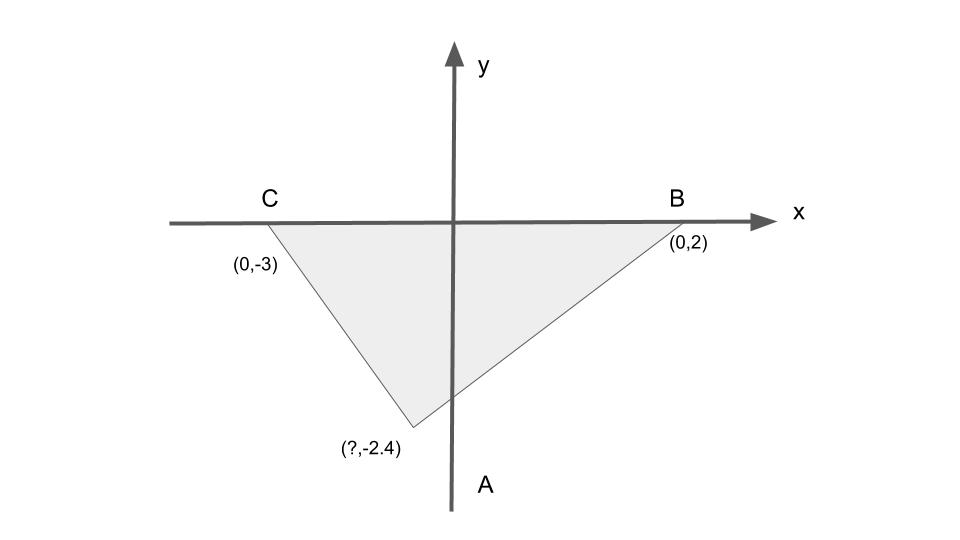
สังเกตุไหมคะว่าจุด $A$ พี่บิวไม่ได้หาค่า $x$ เพราะว่าจุด $A$ เป็นส่วนของความสูงรูปสามเหลี่ยมและอยู่บนแกน $y$ ดังนั้นเรารู้แค่ค่า $y$ ก็เพียงพอแล้วค่ะ

เมื่อเราได้ค่า $A$ $B$ $C$ ครบแล้ว จะได้ ฐาน จาก -3 ถึง 2 เท่ากับ 5
ความสูง คือ ${\frac{12}{5}}$

พื้นที่สามเหลี่ยม $={\frac{1}{2}}$ (ฐาน)(สูง)

  $= {\frac{1}{2}}$ (5)(\frac{12}{5})

  $={\frac{1}{2}}$ (12)

$=6$

จะได้คำตอบคือตัวเลือกที่ 1 เป็นคำตอบของข้อนี้ไปค่ะ

เป็นยังไงบ้างคะกับทวงคะแนนสอบข้อนี้ ขั้นตอนอาจจะเยอะนิดนึงแต่ไม่ยากเลยใช่ไหมคะ ข้อง่ายๆแบบนี้อย่าลืมแชร์ให้เพื่อนๆ #dek62 ได้อ่านด้วยกันนะคะ หากน้องๆมีข้อสงสัยเพิ่มเติม สอบถามมาได้ที่ line @schooldekd หรือ facebook : schooldekd

หากน้องๆ อยากจะติวเรื่องเรขาคณิตวิเคราะห์ให้แม่นขึ้นกว่าเดิม สามารถสมัครเรียนได้ที่ พิชิต TCAS – เรขาคณิต (เรขาคณิตวิเคราะห์ ตรีโกณมิติ เวกเตอร์) สอนโดย อ.กิ๊ฟ  ผศ.ดร.วิทวัชร์ โฆษิตวัฒนฤกษ์ อาจารย์ประจำภาควิชาคณิตศาสตร์ ม.มหิดล ที่มีประสบการณ์การสอนคณิตศาสตร์ในระดับมัธยมศึกษาจนถึงปริญญาเอกทั้งในและต่างประเทศมากกว่า10 ปี  ทั้งยังเป็นตัวแทนประเทศไทยแข่งคณิตศาสตร์โอลิมปิก 3 สมัยโอกาสที่จะได้เรียนกับตัวจริงด้านคณิตศาสตร์แบบนี้มีไม่บ่อยห้ามพลาดนะคะ