อีก 1 สัปดาห์ก็จะถึงวันสอบ PAT1 แล้ววันนี้พี่บิวจาก #พรรคพี่ช่วยน้องสอบติด จะพาน้องๆ ไปทวงคะแนนเมทริกซ์ในข้อสอบ PAT1 เรื่องเมทริกซ์จะออก 2 ข้อแล้วมักจะออกเรื่อง det และพวกสมบัติต่างๆ ของเมทริกซ์ซึ่งข้อสอบไม่ยากมากพี่บิวว่าเป็นเรื่องที่น่าเก็บเรื่องนึงเลยค่ะ ยากง่ายยังไงมาดูกันเลย
ทบทวนสมบัติของเมทริกซ์
– การบวก ลบ คูณด้วยค่าคงที่สมารถดำเนินการตำแหน่งต่อตำแหน่งได้เลย
– เมทริกซ์ไม่มีสมบัติสลับที่การคูณ
– \(A^t\) (ทรานสโพส) คือ การสลับแถวและหลักของ A
– ถ้า \(A={\left[\matrix{a& c\\ b& d}\right]}\) แล้ว \(det(A) = ad-bc\)
– ถ้า \(A={\left[\matrix{a&d&g\\ b&e&h \\c&f&i}\right]}\) แล้ว \(det(A) =(aef+bfg+cdh)-(gec+hfa+idb)\)
– \(A^{-1}\) หาได้ก็ต่อเมื่อ \(det(A)\)\(\not={0}\)
– ถ้า \(A={\left[\matrix{a& c\\ b& d}\right]}\) แล้ว \(A^{-1} =\)\(\frac{1}{det(A)}\)\(\left[\matrix{d& -c\\ -b& a}\right]\)
ตัวอย่างข้อสอบ PAT1 ก.พ.61
กำหนดให้ \(A={\left[\matrix{1& -1\\ 2& 3}\right]}\) และ \(A={\left[\matrix{-3& a\\ 1& b}\right]}\) เมื่อ \(a\) และ \(b\) เป็นจำนวนจริง ถ้า \((A-B)B=B(A-B)\) แล้วค่าของ \(det(A+B)\) เท่ากับข้อใดต่อไปนี้
\(1.\,\,{\frac{-3}{2}}\)\(\,\,\,\,\,\,\,\,\,\,\,\,\,2.\,\,{\frac{-1}{2}}\)\(\,\,\,\,\,\,\,\,\,\,\,\,\,3.\,\,{\frac{5}{2}}\)\(\,\,\,\,\,\,\,\,\,\,\,\,\,4.\,\,{\frac{7}{2}}\)\(\,\,\,\,\,\,\,\,\,\,\,\,\,5.\,\,{\frac{13}{2}}\)
โจทย์ถามว่า \(det(A+B) = ?\)
โจทย์ให้เมทริกซ์ \(A\) กับ \(B\) มาโดยที่ เมทริกซ์ \(B\) ติดตัวแปร \(a ,b\) ไว้หมายความว่าพี่บิวต้องหาค่าของตัวแปร \(a ,b\) มาให้ได้ก่อนถึงจะหา \(det(A+B)\) ได้
จาก \((A-B)B = B(A-B)\) แก้สมการจะได้
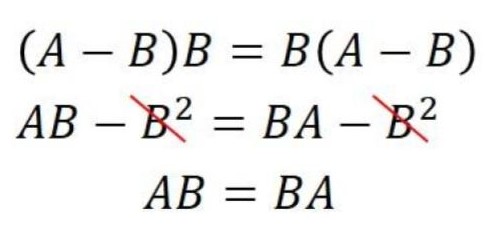
จะได้ว่า \(AB=BA\) แต่อย่าลืมนะคะว่าเมทริกซ์ไม่มีสมบัติการสลับที่การคูณ ดังนั้น \(AB\) จะไม่เท่ากับ \(BA\) เสมอไปค่ะ

ขั้นตอนต่อไปก็แทนค่าเมทริกซ์ \(A\) และ \(B\) ในสมการหลักการคูณเมทริกซ์คือ เอาเมทริกซ์แนวนอนคูณกับเมทริกซ์แนวตั้ง
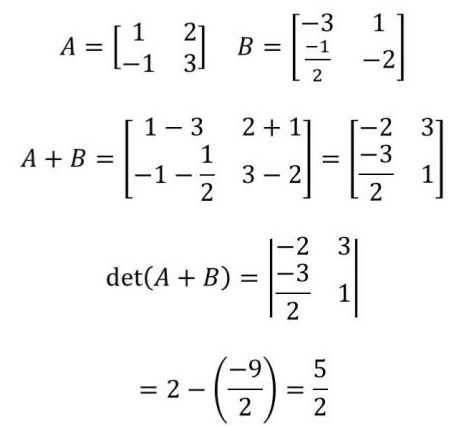
จะเห็นว่าตำแหน่งที่ \(a_{11}\) ของเมทริกซ์ทั้งสองฝั่งสามารถนำมาแก้สมการหา \(a\) ได้และตำแหน่ง \(a_{12}\) สามารถของทั้งสองฝั่งสามารถนำมาแก้หาค่า \(b\) ได้เช่นกัน
เมื่อได้ค่า \(a\) และ \(b\) มาแล้วก็นำไปแทนค่าในเมทริกซ์ \(B\) แล้วหาเมทริกซ์ \(A+B\) ได้เลย
พอได้เมทริกซ์ \(A+B\) มาแล้วก็หา \(det(A+B)\) ได้เลย \(det\) หาได้จากคูณลงลบคูณขึ้น ดังนั้นเราจะได้ค่าของ \(det(A+B) = {\frac{5}{2}}\) เป็นคำตอบของข้อนี้ไปค่ะ
แค่รู้สมบัติก็แก้โจทย์ได้แล้วง่ายๆ แบบนี้อย่าลืมทวงคะแนนคืนมานะคะ
หากน้องๆ มีข้อสงสัยอยากสอบถามเพิ่มเติมสามารถสอบถามมาได้ที่ line @schooldekd หรือ facebook : schooldekd สำหรับน้องๆ ทีม #พรรคนี้อ่านหนังสือไม่ทัน สนใจอยากติวเพิ่มเติมเรื่องเมทริกซ์สามารถสมัครเรียนได้ที่ พิชิต TCAS – รวมบทอิสระ (เซต ตรรกศาสตร์ เมทริกซ์ จำนวนเชิงซ้อน) สอนโดย อ.กิ๊ฟ ผศ.ดร.วิทวัชร์ โฆษิตวัฒนฤกษ์ อาจารย์ประจำภาควิชาคณิตศาสตร์ ม.มหิดล ที่มีประสบการณ์การสอนคณิตศาสตร์ในระดับมัธยมศึกษาจนถึงปริญญาเอกทั้งในและต่างประเทศมากกว่า10 ปี ทั้งยังเป็นตัวแทนประเทศไทยแข่งคณิตศาสตร์โอลิมปิก 3 สมัยโอกาสที่จะได้เรียนกับตัวจริงด้านคณิตศาสตร์แบบนี้มีไม่บ่อยห้ามพลาดนะคะ



