สรุปเข้มจำนวนจริง บทพื้นฐานของคณิต ม.ปลาย ที่น้องๆ ต้องรู้

สวัสดีค่ะน้องๆ ทุกคนกลับมาพบกับบทความฟิตเพิ่มเกรดอีกครั้ง หลังจากห่างหายมานาน วันนี้พี่บิวจะพาน้องๆ ไปพบกับเรื่องจำนวนจริง ซึ่งเป็นเรื่องพื้นฐาน ที่จะถูกนำไปใช้กับเรื่องอื่นๆ มากมายเลยในคณิตศาสตร์ ม.ปลาย เรื่องจำนวนจริงจะมีเนื้อหาบางส่วนที่ทับซ้อนกับคณิตศาสตร์ ม.ต้นอยู่ ถ้าน้องๆ มีพื้นฐานแน่นก็จะสบายไปเลย เนื้อหาในบทจำนวนจริงจะค่อนข้างเยอะ และมีความหลากหลาย 

โครงสร้างของระบบจำนวนจริง

ก่อนอื่นมาดูโครงสร้างของจำนวนจริงกันก่อน จำนวนจริงประกอบไปด้วยจำนวนตรรกยะ และจำนวนอตรรกยะ

• จำนวนตรรกยะ คือ จำนวนที่เขียนเป็นเศษส่วนของจำนวนเต็มได้, ทศนิยมซ้ำ, รากที่ถอดได้ลงตัว 
• จำนวนอตรรกยะ คือ จำนวนที่เขียนเป็นเศษส่วนของจำนวนเต็มไม่ได้, ทศนิยมที่ไม่ซ้ำ, รากที่ถอดได้ไม่ลงตัว, ค่าพิเศษ เช่น \(\pi , e\)

การเท่ากันของจำนวนจริง

การเท่ากันในที่นี้มันก็คือ สมการนั่นเอง เป็นคุณสมบัติพื้นฐานที่จะช่วยให้น้องๆ แก้สมการได้ง่ายขึ้น และ ถ้า \(ab=0\) แล้ว \(a=0\) หรือ \(b=0\)

การมากกว่า และน้อยกว่าของจำนวนจริง

ถ้าการเท่ากัน คือสมการ การมากกว่าและน้อยกว่า ก็คืออสมการนั่นเอง การคูณและการหารตลอดด้วยจำนวนลบจะทำให้เครื่องหมายอสมการกลับข้าง

การบวกและการคูณของจำนวนจริง

สมบัติทั่วไปของการบวกและการคูณจำนวนจริง

การดำเนินการของพหุนาม

เอกลักษณ์ที่ถูกนำไปใช้บ่อยในการแก้สมการพหุนาม หรือ อสมการพหุนาม ถ้าน้องๆ รู้เอกลักษณ์เหล่านี้จะช่วยให้น้องๆ แก้โจทย์ได้ง่ายและเร็วขึ้น

พหุนามคือ พจน์ติดตัวแปรที่เขียนได้ในรูป \(a_n{x^n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+…+{a_1}+a_0\)

• \(n\) คือ ดีกรี หรือ กำลังของพหุนาม
• \(a_n\) คือ สัมประสิทธิ์ของพจน์แรก 

การแยกตัวประกอบพหุนาม

การแยกตัวประกอบพหุนามเป็นหัวใจสำคัญของพหุนามเลย น้องๆ สามารถอ่านวิธีการแยกตัวประกอบแบบละเอียด ได้ที่นี่ คลิกเลย  

สมการพหุนาม

สมการพหุนามกำลังสูงกว่าสอง แก้ได้โดย แยกตัวประกอบลดทอนกำลังไปเรื่อยๆ 

อสมการพหุนาม

ถ้าอสมการพหุนามมีพจน์ที่สูงกว่าสอง ให้พิจารณาเลขชี้กำลัง ถ้ากำลังเป็นคู่ให้แยกคิดต่างหาก และถ้ากำลังเป็นคี่ให้ทอนเหลือ 1

เศษส่วนพหุนาม

สมการเศษส่วนพหุนาม สามารถแก้ตามได้ตามปกติ โดยต้องตรวจคำตอบว่าตัวส่วนไม่เป็น 0

ตัวอย่างโจทย์  อสมการพหุนาม \(\frac{(x-3)^2{(x+1)}(x+2)^3}{(x-2){(x+5)^4}}>0\) 

1. 1. จากโจทย์อีกฝั่งเป็น 0 อยู่แล้ว
   2. จากโจทย์มีกำลังคู่ คือ 2 และ 4 เราจะแยกคิดต่างหาก ดังนั้นเราจะได้ \( x \ne 3\)เพื่อไม่ให้ตัวเศษเป็น 0 และ \( x \ne -5\) เพื่อไม่ให้ตัวส่วนเป็น 0  และกำลังคี่ คือ 1 และ 3 เราจะทอนเป็นกำลัง 1 จะได้ว่า

\(\frac{(x-1)(x+2)}{(x-2)}>0\)

     3. พล็อตค่าบนเส้นจำนวน จะได้ว่า

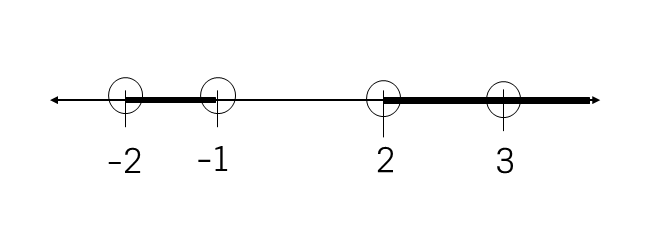
จะได้คำตอบของข้อนี้คือ \((-2,-1) \cup (2,3) \cup (3, \infty)\) ไปนั่นเอง

ค่าสัมบูรณ์

ค่าสัมบูรณ์เปลี่ยนลบให้เป็นบวก สมบัติของค่าสัมบูรณ์ช่วยให้แก้สมการค่าสัมบูรณ์ได้ง่ายขึ้น มาดูตัวอย่างกันเลย

ตัวอย่าง \(|x-3|=5\) 

วิธีที่ 1 : แบ่งกรณี

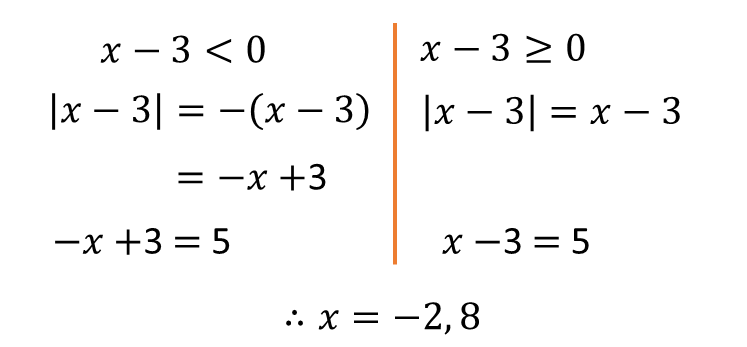
วิธีที่ 2 : ยกกำลังสองทั้งสองข้าง

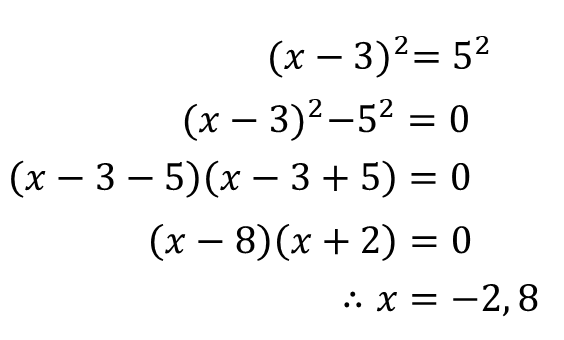
วิธีที่ 3 : แตกเป็น \(p(x)= \pm{q(x)}\)

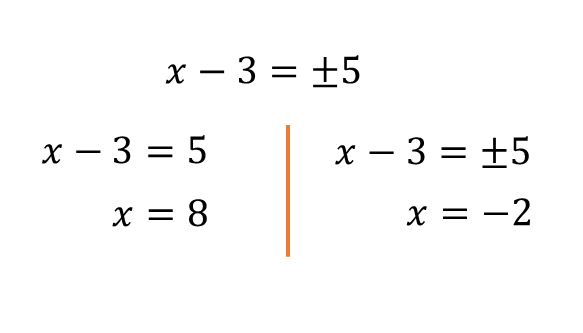
รากที่สอง

ตัวอย่างการถอดรากที่สอง โจทย์คือ \(\sqrt{x+2} = 2\) 

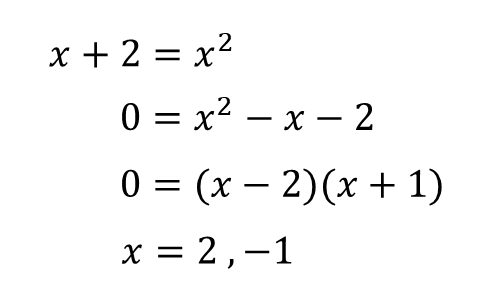
วิธีที่ใช้คือ การยกกำลังสองทั้งสองข้าง ซึ่งข้อนี้คำตอบคือ 2 ตัวเดียวเพราะว่า ถ้านำ -1 ไปแทนในโจทย์ จะทำให้    \(\sqrt{     }\) ติดลบนั่นเอง

จบไปแล้วนะคะ สำหรับสรุปเนื้อหาจำนวนจริง ทั้งหมดนี้พี่บิวเอามาจากคอร์สเก่งคณิตศาสตร์ ม.4 เทอม 1 อ.กิ๊ฟได้สรุปเนื้อหาและเฉลยแบบฝึกหัดให้แบบละเอียดครบถ้วน สมัครเรียนกดที่รูปด้านล่างได้เลย สำหรับวันนี้พี่บิวลาไปก่อน สวัสดีค่ะ

สอบถามเพิ่มเติม และปรึกษาพี่ๆ Dek-D School ได้เลยที่ Line @schooldekd และติดตามข่าวสารการเตรียมตัวสอบได้ที่ช่องทางต่างๆ ต่อไปนี้