ฟิตเพิ่มเกรด คณิต ม.ปลาย – เซต

สวัสดีค่ะน้องๆ ทุกคน ใกล้เปิดเทอมแล้วเป็นไงบ้างคะ พร้อมหรือยัง ถ้ายังไม่พร้อมมาฟิตเพิ่มเกรดกับพี่บิวดีกว่า ฟิตเพิ่มเกรดวันนี้พี่บิวจะพาน้องๆ ไปพบกับเรื่องเซต ซึ่งเป็นเรื่องพื้นฐานอีกเรื่องนึงเลยในวิชาคณิตศาสตร์ เพราะว่าเราจะใช้เซตในการจัดกลุ่มชุดตัวเลข กลุ่มของจำนวนหรือกลุ่มของสิ่งอื่นๆ อีกมากมาย พี่บิวขอบอกก่อนเลยว่าน้องๆ จะได้เจอเซตเยอะแน่ๆ ในข้อสอบเข้ามหาวิทยาลัย ถ้าหากน้องๆ ไม่เข้าใจเซตคงจะไม่ดีแน่เลย เรื่องเซตไม่ยากมาทบ ทวนพร้อมกันกับพี่บิวเลยค่ะ^^

เซตก็เหมือนกับกล่องหรือกระเป๋าที่ใช้เก็บสิ่งต่างๆ ให้อยู่ด้วยกัน สมาชิกของเซตจะต้องชัดเจน ไม่กำกวม บ่งบอกได้เป็นสากล เช่น เซตของสระในภาษาอังกฤษคือ \(\{a, e, i, o, u\}\), เซตของจำนวนจริง เป็นต้น

ทบทวนเรื่องเซต

ให้เซต \(A = \{a, e, i, o, u\}\), \(B = \{e, i, o\}, \,C =  \{a, e, i, o, u\}\), \(D = \{b, c, d\}\)

• เราจะใช้ \(\{\}\) เป็นสัญลักษณ์แทนเซต เช่น \(A = \{a, e, i, o, u\}\)

การเป็นสมาชิกของเซต

• \(e\in A\) คือ \(e\) เป็นสมาชิกของ \(A\) เพราะว่า \(e\) อยู่ในเซต \(A\)
• \(b\notin A\) คือ \(b\) ไม่เป็นสมาชิกของ \(A\)  เพราะว่า \(b\) ไม่อยู่ในเซต \(A\)

การเป็นสับเซตของเซต

• \(B \subset A\) คือ \(B\) เป็นสับเซตของ \(A\) เพราะว่าสมาชิกทั้งหมดของ \(B\) เป็นสมาชิกของ \(A\) ถ้ามีสมาชิกตัวใดตัวนึงของ \(B\) ไม่อยู่ใน \(A\)  \(ฺB\) จะไม่เป็นสับเซตของ \(A\) เลย
• \(D \not\subset A\) คือ \(D\) ไม่เป็นสับเซตของ \(A\) เพราะว่าสมาชิกของ \(D\) ไม่เป็นสมาชิกของ \(A\)

การดำเนินการของเซต

• \(B \cup D\)(ยูเนียน) คือ เซตของการรวม \(B\) และ \(D\) เข้าด้วยกัน เช่น \(B \cup D = \{e,i,o,b,c,d\}\) 
• \(A \cap B\)(อินเตอร์เซกชัน) คือ เซตของสมาชิกร่วมกันของ \(A\) และ \(B\) เช่น \(A \cap B = \{e, i, o\}\)
• \(A – B\)(ลบ) คือ เซตของสมาชิกที่อยู่ใน \(A\) แต่ไม่อยู่ใน \(B\) เช่น \(A – B = \{a,u\}\)
• \(A^ \prime\)(คอมพลีเมนต์) คือ เซตของสมาชิกที่ไม่อยู่ใน \(A\)

จำนวนสมาชิกของเซต

• \(n(A)\) คือ จำนวนสมาชิกของ \(A\) มี 5 ตัวคือ \(a, e, i, o, u\)

เพาเวอร์เซต

• \(P(B)\) คือ เซตของสับเซตทั้งหมดของ \(B\) คือ \(\{\{e\},\{i\},\{o\},\{e,i\},\{e,o\},\{i,o\},\{e,i,o\},∅\}\) และถ้า \(B\) มีสมาชิก \(n\) ตัว \(P(B)\) มีสมาชิก \(2^n\) ตัว เช่น \(b\) มีสมาชิก 3 ตัว \(P(B)\) มีสมาชิก \(2^3 = 8\) 

การเท่ากันของเซต

• \(A = C\) ก็ต่อเมื่อ สมาชิกทุกตัวของ \(A\) เป็นสมาชิกของ \(C\) และ สมาชิกทุกตัวของ \(C\) เป็นสมาชิกของ \(A\) หรือ \(A = C\) ก็ต่อเมื่อ \(A \subset C\) และ \(C \subset A\)

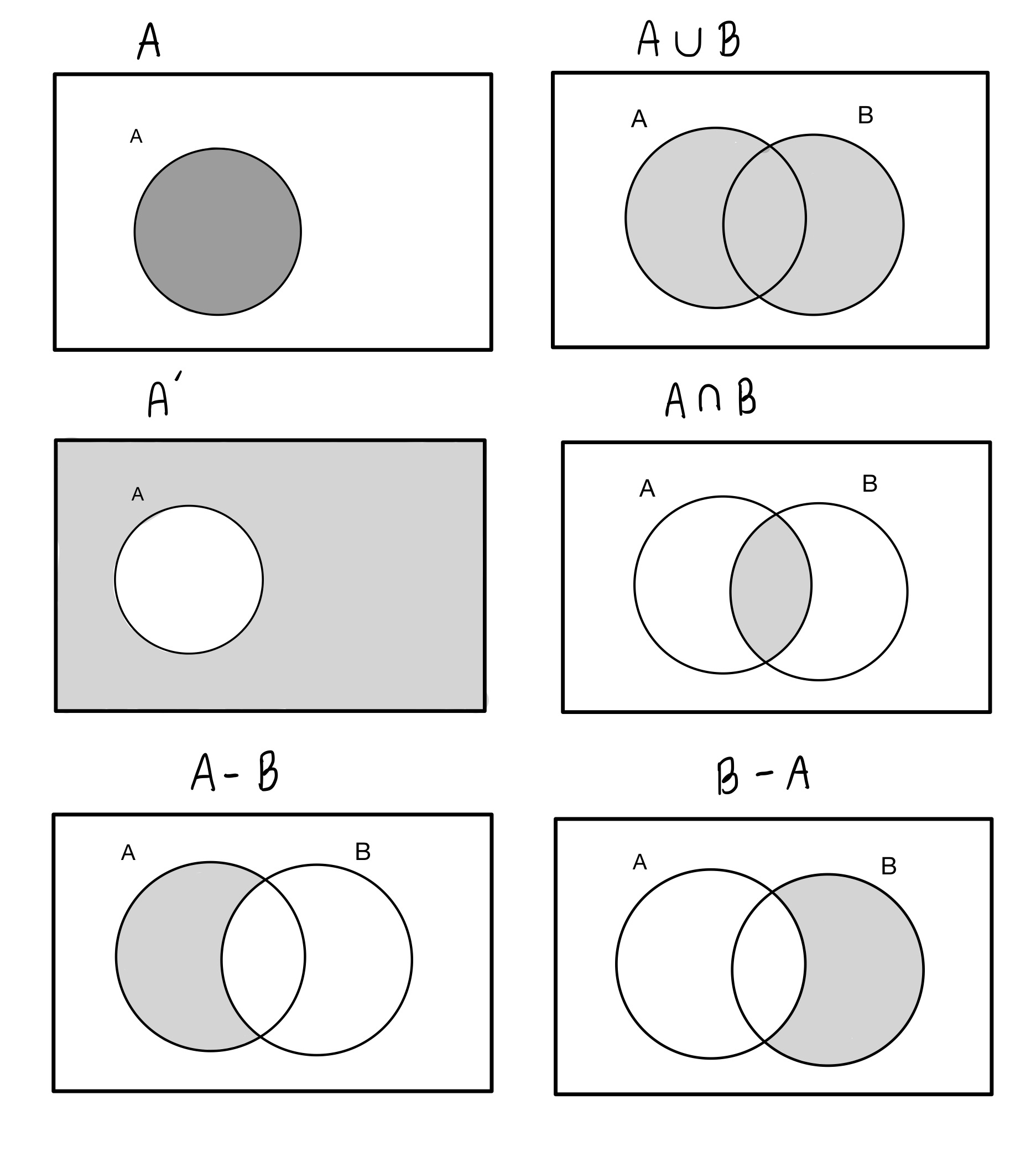
แผนภาพเวนน์ – ออยเลอร์

แผนภาพเวนน์ – ออยเลอร์ คือเอาเซตมาเขียนเป็นรูปภาพนั่นเอง แผนภาพช่วยให้เราดูเซตได้ง่ายขึ้น และยังสะดวกต่อการคำนวณเซตอีกต่างหาก เช่น

ฟิตเพิ่มเกรดคณิตศาสตร์คราวหน้าพี่บิวจะมาอธิบายเรื่องการหาจำนวนสมาชิกของเซต และพาน้องๆ ไปเจอกับโจทย์เซตที่ยากขึ้นอีก รอติดตามได้เลยและถ้าหากน้องๆ มีข้อสงสัยอยากสอบถามพี่บิวเพิ่ม สอบถามมาได้เลยที่ line @schooldekd หรือ facebook Dek-D School พี่บิวยินดีเป็นที่ปรึกษาและตอบทุกถามที่น้องๆ สงสัยเลยนะคะ

และถ้าน้องๆ อยากเข้าใจเรื่องเซตอย่างถ่องแท้พี่บิวแนะนำ คอร์ส เก่งคณิตศาสตร์ ม.4 เทอม 1 และคอร์ส พิชิต TCAS – รวมบทอิสระ (เซต ตรรกศาสตร์ เมทริกซ์ จำนวนเชิงซ้อน) สอนโดย อ.กิ๊ฟ ผศ.ดร.วิทวัชร์ โฆษิตวัฒนฤกษ์ อาจารย์ประจำภาควิชาคณิตศาสตร์ ม.มหิดล ที่มีประสบการณ์การสอนคณิตศาสตร์ในระดับมัธยมศึกษาจนถึงปริญญาเอกทั้งในและต่างประเทศมากกว่า10 ปี  ทั้งยังเป็นตัวแทนประเทศไทยแข่งคณิตศาสตร์โอลิมปิก 3 สมัยอีกต่างหาก

อ.กิ๊ฟ ได้สอนเซตไว้อย่างละเอียดพร้อมทั้งยกตัวอย่างให้เข้าใจได้ง่ายอีกด้วย โอกาสที่จะได้เรียนกับตัวจริงด้านคณิตศาสตร์แบบนี้มีไม่บ่อย ห้ามพลาดนะคะ 😀