ฟิตเพิ่มเกรด ฟิสิกส์ ม.ปลาย – การแตกแรง

สวัสดีวันศุกร์สุดสัปดาห์นะคะ น้องๆ ทุกคนเป็นไงบ้างคะ ไปดู Avengers กันหรือยัง ถ้ายังระวังโดนสปอยล์นะคะ 😀 มาเข้าเรื่องของเราดีกว่า ฟิตเพิ่มเกรดวันนี้พี่บิวจะมาสอนน้องๆ เรื่องการแตกแรงหรือการแตกเวกเตอร์ ซึ่งการแตกแรงเนี่ยจะถูกนำไปใช้ประโยชน์ในวิชาฟิสิกส์เยอะมาก ทั้งเรื่องกฎการเคลื่อนที่ของนิวตัน โพรเจคไทล์ การเคลื่อนที่แบบหมุน ซึ่งถ้าน้องๆ ทำไม่ได้พี่บิวว่าลำบากแน่ ว่าแล้วมาดูกันเลยดีกว่าว่าการแตกแรงทำยังไง

ค่ามุมที่ควรรู้

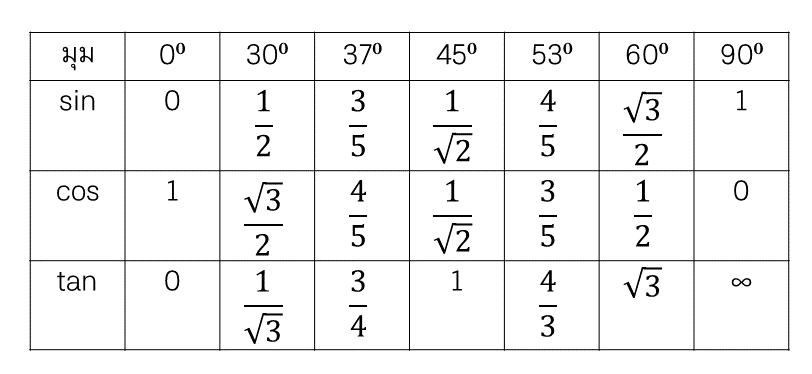
ส่วนเรื่องวิธีการจำค่ามุมพี่บิวว่าน้องๆ คงจะรู้จักการหาค่ามุมจากมือซ้าย หรือดูจากรูปสามเหลี่ยมมุมฉาก น้องๆ สามารถดูหลักการจำค่ามุมได้จาก คลิก

การแตกแรง

การแตกแรง คือ การที่แรงมีทิศทางที่ไม่เป็นแนวตรง (คือเอียงๆ นั่นเองค่ะ) ให้เป็นเส้นตรงตามแนวแกน x แกน y ซึ่งแน่นอนถ้ามันเอียงมันก็ต้องมีมุมใช่ไหมคะ ตอนนี้เลยค่ะ ที่มุมที่พี่บิวให้ไปตอนแรกได้ถูกนำมาใช้ประโยชน์แล้ว

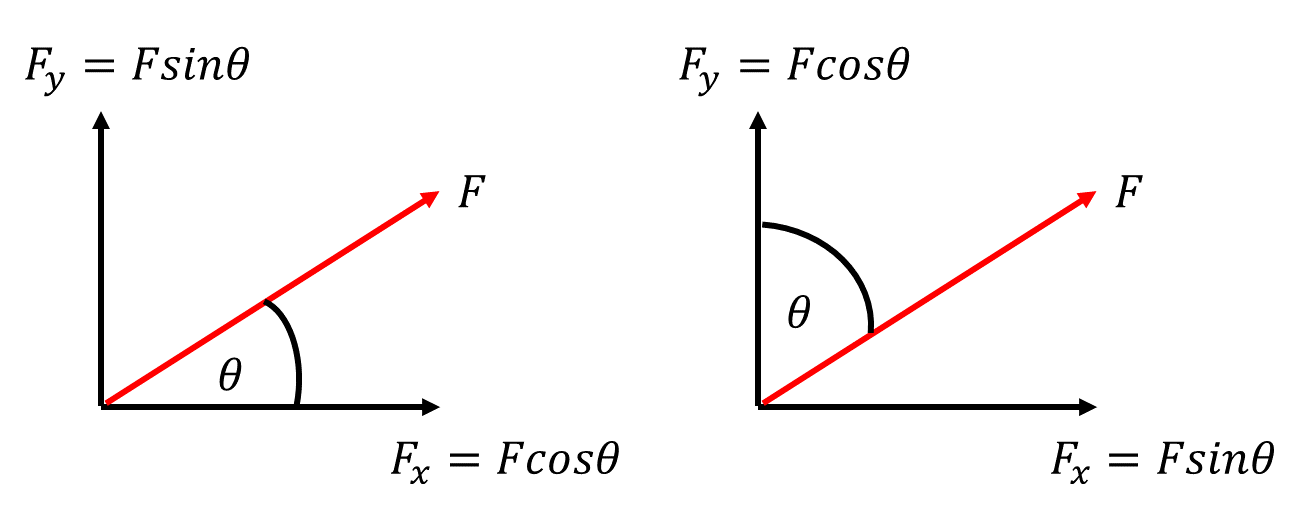
หลักการแตกแรงก็ง่ายๆ เลย คือ “ใกล้มุมเป็น cos ไกลมุมเป็น sin” บอกอย่างนี้อาจจะงงเรามาสังเกตจากรูปกันเลย

รูปแรก มุมอยู่ใกล้กับเส้นแกน x (แนวนอน) จึงแตกมุมแกน x เป็น cos และเส้นแกน y (แนวตั้ง) ไม่อยู่ติดมุมจึงแตกมุมเป็น sin

รูปที่ 2 มุมอยู่ติดแกน y แตกแรงเป็น cos และแกน x ไม่อยู่ใกล้มุมจึงแตกแรง sin

คอนเซ็ปต์ง่ายๆ เลยใช่ไหมคะ แค่นี้ก็แตกแรงได้แบบสบายๆ แล้วเพื่อเพิ่มความเข้าใจเรามาดูตัวอย่างโจทย์กันเลยดีกว่าค่ะ

ตัวอย่างโจทย์

มวล 10 kg ไถลลงจากพื้นเอียงดังรูป จงแตกแรงของมวล m

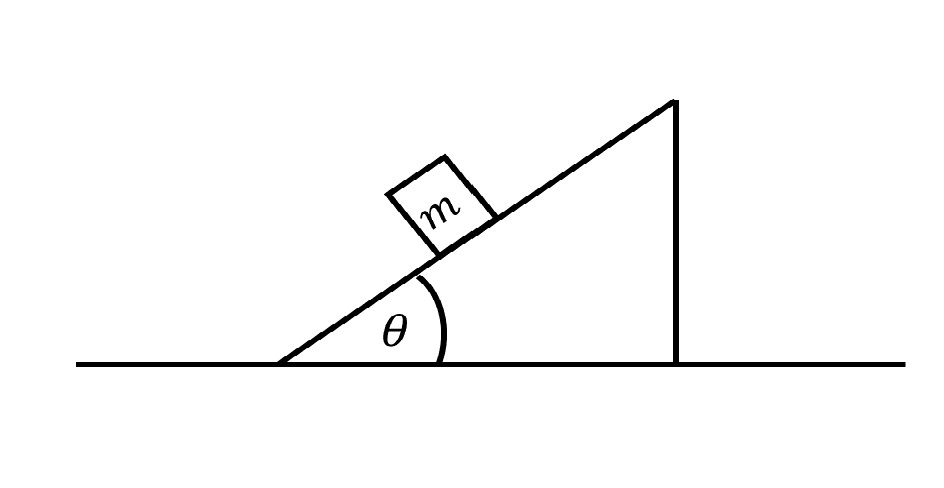
จากโจทย์ มวล m กระทำกับพื้นเอียง เกิดเป็นแรง mg (เนื่องจากแรงโน้มถ่วงของโลก)และแรง mg นี่แหละที่เราจะแตกแรงของมัน จากนั้นเขียนแตกแกน x แกน y ออกมา (เพราะว่าเป็นพื้นเอียงเราก็เลยมองแกน x แกน y ได้ยากนิดนึง ถ้าน้องๆ ลองหมุนรูปดูจะเห็นว่า mg คือแรงส่วนที่เอียงๆ ที่เราต้องแตก)

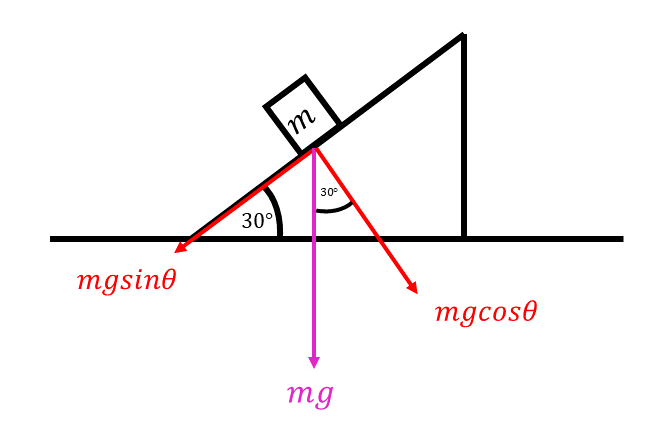จากวิธีการแตกแรงคือ “ใกล้มุมเป็น cos ไกลมุมเป็น sin” แต่มุมที่เรามีในโจทย์มันเป็นมุมของรูปสามเหลี่ยม แล้วเราจะใช้มุมไหนเป็นตัวบอกล่ะ ว่าเส้นไหนใกล้มุม เส้นไหนไกลมุม วิธีการคือให้ใช้มุมไหนก็ได้ ถ้าน้องๆ ใช้มุมเดียวกันกับพี่บิวค่ามุมก็จะเท่ากับมุมของรูปสามเหลี่ยม (เพราะว่าเป็นมุมแย้งกัน) และถ้าน้องๆ ใช้อีกมุมนึง ค่ามุมต้องเป็น \(60^\circ\) (เพราะว่ามุมภายในรูปสามเหลี่ยมเท่ากับ \(180^\circ\) นั่นคือ \(90^\circ\)\(-30^\circ\) = \(60^\circ\) นั่นเอง)

เอาล่ะ เมื่อได้ทุกอย่างพร้อมแล้ว เรามาแตกแรงกันดีกว่า เส้นสีแดงด้านขวาคือเส้นที่อยู่ใกล้มุม เราจะแตกได้เป็น \(mgcos\theta\) และเส้นสีแดงด้านซ้ายซึ่งอยู่ไกลมุมเราจะแตกได้เป็น \(mgsin\theta\)

จาก \(m = 10 ,\,\)\(\,g = 10,\,\) \(cos30^\circ = \frac{\sqrt{3}}{2},\,\)  \(sin30^\circ = \frac{1}{2}\)

ดังนั้น \(mgcos\theta\) จะได้ \(10(10)cos30^\circ = 10(10)(\frac{\sqrt{3}}{2}) = 50\sqrt{3}\)  

และ  \(mgsin\theta\) จะได้ \(10(10)sin30^\circ = 10(10)(\frac{1}{2}) = 50\)

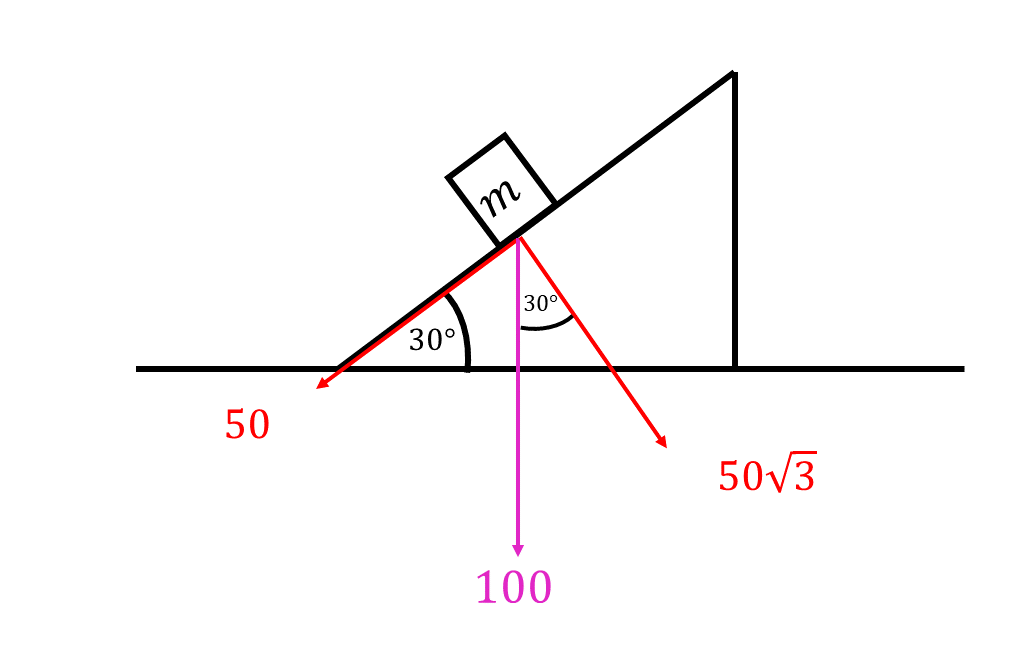
แค่นี้เราก็ได้คำตอบออกมาแล้ว ไม่ยากเลยใช่ไหมคะ ถ้าน้องๆ มีข้อสงสัยเพิ่มเติมอยากสอบถาม สามารถสอบถามพี่บิวเข้ามาได้เลยที่ line @schooldekd หรือ facebook Dek-D School

น้องๆ ที่กำลังจะขึ้น ม.ปลาย อยากเตรียมความพร้อมก่อนใคร พี่บิวแนะนำคอร์สเก่งฟิสิกส์ ม.4 เทอม 1 และสำหรับน้องๆ ที่เตรียมตัวสอบเข้ามหาวิทยาลัยพี่บิวก็มีคอร์สที่สรุปเนื้อหาของฟิสิกส์พร้อมทั้งตะลุยโจทย์ให้น้องๆ ได้ฝึกและเตรียมความพร้อมกับคอร์สพิชิต TCAS ฟิสิกส์ สอนโดย อ.หลิน ดร.สลิลพร กิตติวัฒนากูล อ.พิเศษภาควิชาวิศวกรรมและวิทยาศาสตร์วัสดุ University of Virginia มหาวิทยาลัยชั้นนำของสหรัฐอเมริกาและอ.ประจำภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย

ได้เรียนกับตัวจริงด้านฟิสิกส์แบบนี้มีไม่บ่อย พลาดไม่ได้แล้วนะคะ ฟิตเพิ่มเกรดฟิสิกส์คราวหน้ามาพบกับพี่บิวอีกครั้งกับเรื่องหลักการจำค่ามุม สำหรับวันนี้พี่บิวขอลาไปก่อน สวัสดีค่ะ